- In order to find the ith smallest of n elements, one naive approach is to sort the n elements using merge sort or heap sort and pick the ith element, which would take O(NlgN) time in the worst case.
Randomized Divide-and-Conquer Algorithm
- Instead we could use a randomized divide-and-conquer algorithm.
- In this algorithm, we do not sort the sub arrays which are consisted of elements smaller than the pivot and elements bigger than the pivot.


- If we're lucky, we could shrink the range exponentially with ratio such as 9/10.
- If we're unlucky, all the elements would go to one of the partitions, and would result selecting the pivot n times.
- Therefore the overall runtime in worse case is even worse, O(N^2).
- Using indicator variable, Xk = 1 if PARTITION generates a k:n-k-1 split and 0 otherwise, we could analyze the average run time.
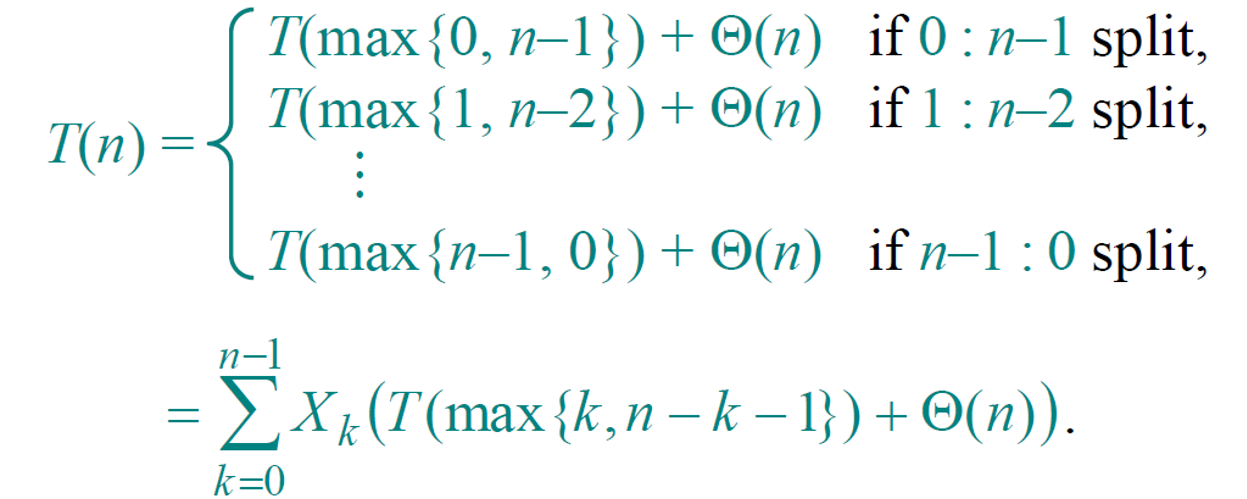
- The overall proving procedure is similar to proving the depth of a random BST.

- Using induction, we can show that the expected runtime is O(N).
Linear time Randomized Divide-and-Conquer Algorithm
- The key idea to improve the algorithm to have O(N) runtime even in the worst case is to choose a good pivot recursively.

- 1. takes O(n) run time.
- 2. takes T(n/5) run time.
- 3. takes O(n) run time.
- 4. takes T(3n/4) run time.
- Using these technique, at least 3(n/10) elements are smaller than x and 3(n/10) elements are bigger than x.

- In practice, this algorithm runs slowly, because the constant in front of n is large.
- The randomized algorithm is far more practical.
'Algorithms & ICPC' 카테고리의 다른 글
| Greedy (0) | 2021.10.17 |
|---|---|
| Dynamic Programming (0) | 2021.10.14 |
| Trees (0) | 2021.10.13 |
| Linear Sorting (0) | 2021.09.27 |



